OLOÏDE
Les références à cette page sont essentiellement
tirées de la traduction (personnelle) de certaines pages du
document "The Developement of the Oloid" de Hans Dirnböck et
Hellmuth Stachel, 1997 Heldermann Verlag (ISSN 1433-8157). Les pages 105-118 sont disponibles en doc pdf. |
|
|
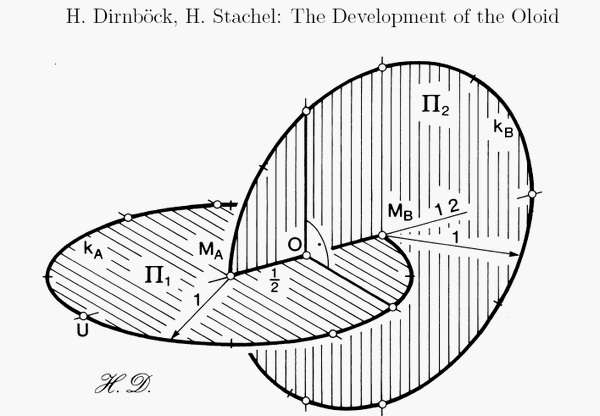
Considérons deux cercles kA, kB, dans des plans perpendiculaires, tels que kA passe par le centre MB de kB et kB passe par le centre MA de kA. |
|
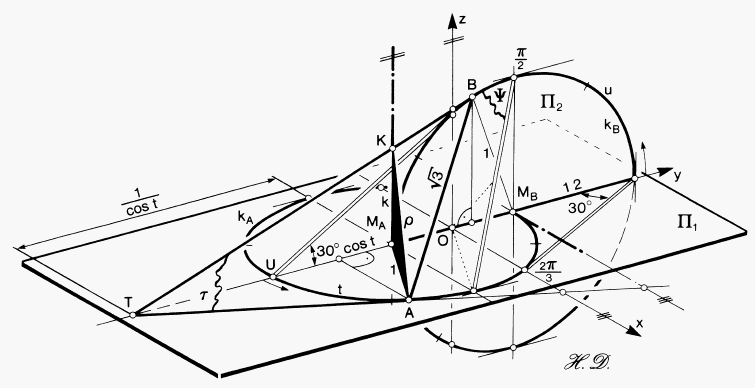
Le point T appartient à la ligne 12, qui est l'intersection des deux plans perpendiculaires
P1 et P2. T est aussi le point d'intersection de la tangente au cercle kA en A et de la tangente au cercle kB en B. Si un plan T contient ces deux tangentes, donc s'il touche le cercle kA en A et le cercle kB en B, alors le segment AB est une génératice de la surface de l'oloïde. |
 |
| Ci-contre, deux animations présentant la génératice de l'oloide (à partir du cube invertible de Paul Schatz) et le solide. ref. : http://www.fzk.at/timeform_oloid.html |
  |
|